Why Do Large Sample Sizes Result In Smaller Standard Errors?
How To Calculate The Sample Size Given The Confidence Level \U0026 Margin Of Error
Keywords searched by users: Why do large sample sizes produce smaller standard errors what is the formula for calculating the standard error of the sample mean when the sample size is n?, Standard error vs standard deviation, Standard error formula, why does standard deviation decrease with sample size, why does standard deviation increase with sample size, Why does the standard error of the mean decrease as the sample size n increases, Standard error of the mean, The advantage of large sample size
Why Does A Larger Sample Size Decrease Standard Error?
The standard error decreases as the sample size increases due to a fundamental statistical principle. When you have a larger sample size, it allows for a more accurate representation of the entire population. This happens because, as the sample size approaches the true size of the population, the individual sample means become increasingly concentrated around the actual population mean. In other words, when you take a larger sample, you’re more likely to get results that are very close to the true characteristics of the entire population. This reduction in variability leads to a decrease in the standard error, making your estimates more reliable. This statistical phenomenon is crucial for drawing meaningful conclusions from data and is a cornerstone of statistical analysis.
Does A Larger Sample Size Increase Error?
The relationship between sample size and margin of error is inverse, meaning that as the sample size increases, the margin of error decreases. This is due to the fact that with a larger sample size, there is a more comprehensive representation of the population, leading to more accurate and reliable results. In other words, the margin of error is reduced because there is a higher level of confidence in the findings when a larger number of data points are considered. Therefore, increasing the sample size is a crucial factor in reducing sampling error and obtaining more precise conclusions in statistical analysis.
Does The Standard Error Become Smaller Simply By Increasing The Sample Size?
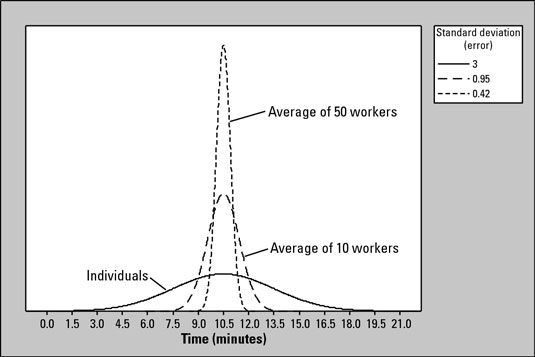
Does the standard error decrease as the sample size increases? The variations in the curves indicate variations in the standard deviation of the sampling distribution. It is observed that smaller sample sizes typically result in larger standard errors, whereas larger sample sizes tend to yield smaller standard errors. To illustrate this point about standard errors in a different manner, consider the following example:
Details 8 Why do large sample sizes produce smaller standard errors


:max_bytes(150000):strip_icc()/SamplingError-4189704-Final-533c7191287b4b0e89fb11873679e08c.jpg)


Categories: Collect 99 Why Do Large Sample Sizes Produce Smaller Standard Errors
See more here: future-user.com

The standard error measures the dispersion of the distribution. As the sample size gets larger, the dispersion gets smaller, and the mean of the distribution is closer to the population mean (Central Limit Theory). Thus, the sample size is negatively correlated with the standard error of a sample.Standard error decreases when sample size increases – as the sample size gets closer to the true size of the population, the sample means cluster more and more around the true population mean.The relationship between margin of error and sample size is inverse i.e when sample size increases, the sampling error decreases. This is because the more information you have, the more accurate the results would be.
Learn more about the topic Why do large sample sizes produce smaller standard errors.
- How is Sample Size Related to Standard Error, Power …
- A beginner’s guide to standard deviation and standard error
- If the sample size increases, the sampling error . – Toppr
- 1. The first reason to understand why a large sample size is beneficial is …
- Statistics Notes: Standard deviations and standard errors – PMC – NCBI
- 7.2: Using the Central Limit Theorem – Statistics LibreTexts
See more: https://rausachgiasi.com/your-money blog